Mathematical Foundations of Machine Learning: Tensors, Scalar tensors, Vectors & Vector transposition

Previously, I described linear algebra, including providing examples of linear equation system and how we can go about solving them either graphically or algebraically.

Now, let’s get started with the fundamental building block of linear algebra for absolutely any kind of machine learning i.e. the Tensors.

So what are Tensors? We hear about tensors associated with Machine Learning in some places and it’s even in the name of TensorFlow, one of the most popular libraries for doing Machine Learning.

“Tensors are simply a Machine Learning specific generalization of vectors and matrices to any number of dimensions”

Well, the zero-dimensional Tenser is a scalar, so it’ll contain just a single value, and then we have vectors which are a linear array in one dimension of values known as vectors, and then a matrix which is a two-dimensional array, a cube can be an example of a three-dimensional tensor.

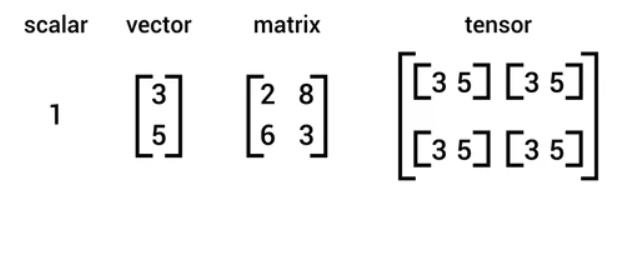
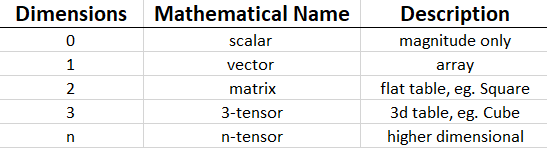
The idea of a tensor is that it generalizes these kinds of objects to any number of dimensions.

Now that we know what Tensors are in general, let’s dig into particular types of them, starting with Scalar Tensors.

Scalar Tensors

Scalars are characterized by having no dimensions, so they are a single numeric value.

So here is a very quick example where I’ve created a 0-dimension tensor

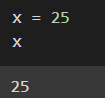
Now using the PyTorch library to make them feel and behave like NumPy arrays, the advantage of PyTtorch tensors relative to the NumPy arrays is that they allow us to have many parallel matrix operations and were designed for rendering graphics and video games or doing video processing, that kind of thing. But they are also used widely in training deep learning algorithms.

Creating a scalar-tensor with PyTorch

So as discussed above scalars have no dimensionality.

Now let’s look at doing the same thing in TensorFlow, here the tensors are created with a wrapper

Creating a scalar-tensor using tf.Variable wrapper in TensorFlow

So, by looking at the shape it is now clear that scalar tensors have no dimensionality just like scalar tensors in PyTorch.

Now let’s take a route towards one-dimensional tensors, more commonly known as vectors.

Vector Tensors

Vectors are a one-dimensional array of numbers and are arranged in an order, so all the elements in the vector are in a specific order, and then we can access each one of the elements in that vector by its index.

Having introduced vectors let’s talk about the most simple operation, which we perform very often on vectors, and this vector transposition. Transposition transforms a vector from a row vector to a column vector or vice versa. So all of the elements in a vector remain intact when we transpose it and they remain in order simply.

Now let’s create a simple vector

creating vector using NumPy array function

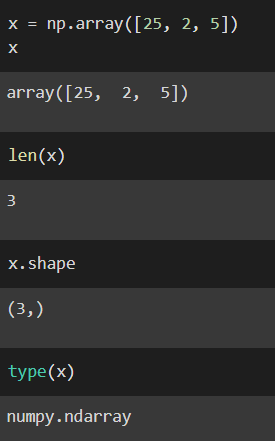
Now let’s look at transposing a vector in numbers. A common operation that NumPy provides is this “.T” that we can add onto the end of any given vector and it will transpose it for us.

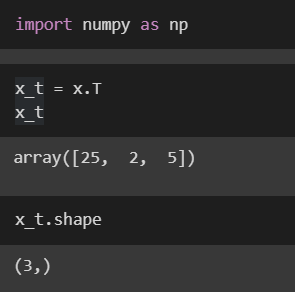
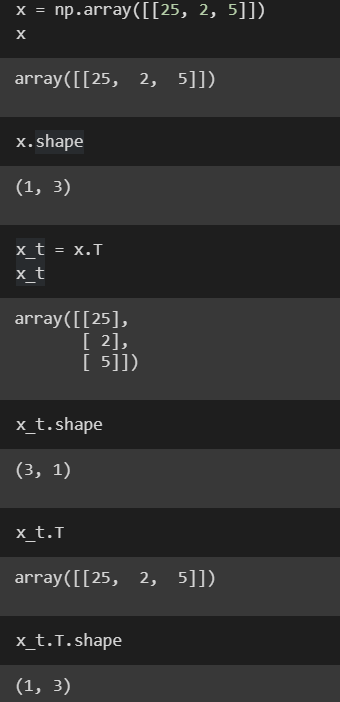
Transposing a regular 1-D array has no effect, but it does when we use nested “matrix-style” brackets because it can transpose a matrix with a dimension of length 1,

Vector transposition

A quick note on zero vectors: These are vectors that consist entirely of zeros and can be created using the number NumPy zeros method.

Zero vector

A final little bit is about creating vectors using PyTorch and TensorFlow the same we used to create scalar tensors, we specify the elements that we’d like to have in our vector in the same way that we have done in NumPy

Defining vectors using PyTorch and TensorFlow